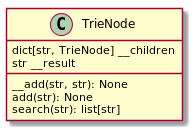
Basis-Datenstruktur: Der einfache Trie (Präfixbaum)
Ein Trie – die Kurzform von »Retrieval« – ist eine einfache Datenstruktur, mit der man in Zeichenketten suchen kann. Ein anderer Begriff dafür ist der »Präfixbaum«. Heute erkläre ich kurz, was man mit einem solchen Teil anstellen kann und wie man es implementiert.
Wozu das Ganze?
Tries können dabei helfen, schnell in vorgegebenen Begriffen zu suchen. Dabei genügt es sogar, nur den Anfang eines Suchworts anzugeben, um Suchergebnisse zu erhalten. Kleines Beispiel: In unserer Liste an Suchbegriffen stehen diese Worte:
- Hallo
- Welt
- HAL 8999
- Halogenlampe
Suchen wir nun nach »hal«, erhalten wir als Ergebnis »Hallo«, »HAL 8999« und »Halogenlampe«.
Wie sieht so eine Datenstruktur aus?
Zunächst baut man mit allen möglichen Suchbegriffen, in denen man suchen möchte, eine Baumstruktur auf. Warum Baumstruktur? Klassische Arrays/Listen sind bei vielen Begriffen unpraktisch, da sie sich nur teuer durchsuchen lassen. In der Baumstruktur verzweigt man immer dann neu, wenn ein Begriff sich von einem bereits vorhandenen Begriff unterscheidet. Somit erreicht man auch eine gewisse Kompression, da für die Begriffe »Hallo«, »HAL 8999« und »Halogenlampe« die ersten drei Zeichen (H, A, L) nur einmal im Baum abgelegt werden müssen.
Klingt kompliziert? Ist aber ganz einfach. Die folgende Animation zeigt einen Beispiel-Baum für die Begriffe »Hallo«, »Haus«, »Welt« und »Wasser«.
Wie funktioniert nun die Suche?
Spielen wir die Suche nach »HAU« durch, die als Ergebnis »Haus« ergeben soll:
Hier sehen wir eine weitere Eigenschaft von Tries: Da die von mehreren Einträgen genutzten Anfänge (Präfixe) nur einmal in der Datenstruktur abgelegt werden, erreicht man eine gewisse Kompression, da keine Redundanzen an den Anfängen entstehen.
Würden wir nur nach »HA« suchen, wäre das Ergebnis »Hallo« und »Haus«:
Eigentlich ganz einfach. Zeit, damit zu spielen.
Der (ganz) einfache Trie
Fangen wir klein an: Bauen wir einen Trie, der genau so aussieht, wie in der Animation dargestellt.
Modellierung eines Knotens
Wir benötigen zuerst das Modell eines Knotens. Dieser Knoten muss Kinder haben können und sollte über Methoden verfügen, die das Hinzufügen eines Begriffs (add(str)) und das Suchen (search(str)) ermöglichen. Außerdem benötigt er ein Feld, in dem ein Ergebniswert (in diesem einfachen Fall unser Begriff) abgelegt werden, wenn am betreffenden Knoten eines vorliegt (in der Animation sind das die Worte in den grünen Rahmen):
In Python ausgedrückt (Python 3, ohne private Methoden – die kommen später noch):
class TrieNode(object):
def __init__(self):
self.__children = {}
self.__result = None
def add(self, word: str) -> None:
pass
def search(self, word: str) -> list:
pass
Zusätzlich entwickeln wir noch ein wenig »Drumherum«, um entsprechend ausprobieren zu können:
root_node = None
class TrieNode(object):
def __init__(self):
self.__children = {}
self.__result = None
def add(self, word: str) -> None:
pass
def search(self, word: str) -> list:
pass
def index_and_search(words: list, search: str):
pass
Implementierung einer einfachen Suche – simple_trie.py
In einem anderen Artikel habe ich die Vorzüge von Doctest beschrieben – und so bietet sich für die Methode index_and_search die Ausstattung mit Doctests an:
def index_and_search(words: list, search: str) -> list:
"""
Indiziere Suchbegriffe und suche anschließend darin
:param list[str] words: Begriffe, aus denen ein Trie aufgebaut werden soll
:param str search: Begriff, nach dem gesucht werden soll
:return: Liste mit Treffern
:rtype: list[str]
Tests:
Aus dem Beispiel:
>>> set(index_and_search(['Hallo', 'Haus', 'Welt', 'Wasser'], 'hau')) == {'HAUS'}
True
Mehrere Treffer:
>>> set(index_and_search(['Hallo', 'Haus', 'Welt', 'Wasser', 'HAL 8999'], 'hal')) == {'HALLO', 'HAL 8999'}
True
Keine Treffer:
>>> index_and_search(['Hallo', 'Haus', 'Welt', 'Wasser', 'HAL 8999'], 'sonne')
[]
"""
Da wir zunächst nicht wissen, in welcher Reihenfolge die Suchergebnisse in der Zielliste stehen werden, verwenden wir für die Doctests als kleinen Workaround set (siehe auch die dazugehörige Dokumentation). Die Reihenfolge ist für uns zum aktuellen Zeitpunkt sowieso irrelevant.
Erwartungsgemäß bringt nun das Ausführen der Tests mit dem Kommandozeilenbefehl…
$ python3.5 -m doctest simple_trie.py
… entspechende Fehler:
**********************************************************************
File "/home/juergen/work/trie-blog/simple_trie.py", line 48, in simple_trie.index_and_search
Failed example:
set(index_and_search(['Hallo', 'Haus', 'Welt', 'Wasser'], 'hau')) == {'HAUS'}
Exception raised:
Traceback (most recent call last):
File "/usr/lib/python3.5/doctest.py", line 1320, in __run
compileflags, 1), test.globs)
File "<doctest simple_trie.index_and_search[0]>", line 1, in <module>
set(index_and_search(['Hallo', 'Haus', 'Welt', 'Wasser'], 'hau')) == {'HAUS'}
TypeError: 'NoneType' object is not iterable
**********************************************************************
File "/home/juergen/work/trie-blog/simple_trie.py", line 52, in simple_trie.index_and_search
Failed example:
set(index_and_search(['Hallo', 'Haus', 'Welt', 'Wasser', 'HAL 8999'], 'hal')) == {'HALLO', 'HAL 8999'}
Exception raised:
Traceback (most recent call last):
File "/usr/lib/python3.5/doctest.py", line 1320, in __run
compileflags, 1), test.globs)
File "<doctest simple_trie.index_and_search[1]>", line 1, in <module>
set(index_and_search(['Hallo', 'Haus', 'Welt', 'Wasser', 'HAL 8999'], 'hal')) == {'HALLO', 'HAL 8999'}
TypeError: 'NoneType' object is not iterable
**********************************************************************
File "/home/juergen/work/trie-blog/simple_trie.py", line 56, in simple_trie.index_and_search
Failed example:
index_and_search(['Hallo', 'Haus', 'Welt', 'Wasser', 'HAL 8999'], 'sonne')
Expected:
[]
Got nothing
**********************************************************************
1 items had failures:
3 of 3 in simple_trie.index_and_search
***Test Failed*** 3 failures.
Doch wie können wir nun den Baum befüllen? Zunächst benötigen wir einen Wurzelknoten, an dem alle Begriffe »angehängt« werden, wie in der Animation gezeigt. Diesem Knoten fügen wir dann alle Worte hinzu. Das alles findet in der Methode index_and_search statt:
global root_node
root_node = TrieNode()
[root_node.add(w) for w in words]
Mittels [root_node.add(w) for w in words] wird die Methode add des Objekts root_node für jeden Eintrag aus der Liste words aufgerufen – eine Abkürzung für die Schreibfaulen. Für den Aufruf der Suche und das Zurückliefern der Treffer fehlt dann noch eine Zeile:
return root_node.search(search)
Nun müssen wir uns weiter um die TrieNode-Klasse kümmen. Hier gibt es noch zwei Methoden zu befüllen. Zunächst muss die add-Methode implementiert werden, um unseren Suchindex aufzubauen. In der Animation konnte man den grundsätzlichen Ablauf schon erkennen:
Im Detail können wir das etwas eleganter lösen. Wir erstellen zusätzlich zur add-Methode noch eine private __add-Methode, mit der wir an jedem Knoten nur noch den »Rest« des verbliebenen Wortes aufarbeiten.
Der erste Aufruf der __add-Methode, der wir das ursprüngliche Wort und den zu verarbeitenden Rest übergeben, geschieht dann in der ursprünglichen add-Methode, wobei anfangs Rest und Wort identisch sind:
def add(self, word: str) -> None:
self.__add(word, word)
Die weitere Verarbeitung sieht dann in der __add-Methode so aus:
def __add(self, word: str, rest: str) -> None:
if len(rest) > 0: # 1.
letter = rest[0].upper() # 2.
if letter not in self.__children.keys(): # 3.
self.__children[letter] = TrieNode() # 4.
self.__children[letter].__add(word, rest[1:]) # 5.
else:
self.__result = word.upper() # 6.
In Worten:
- Wenn noch etwas vom Suchwort übrig ist,
- schnappe den ersten Buchstaben vom Rest – als Großbuchstaben
- und prüfe, ob es noch kein passendes Kind gibt,
- erzeuge es (wenn es noch keines gibt),
- und rufe für das Kind die
__add-Methode auf mit dem Wort und dem Rest ohne den ersten Buchstaben. - Falls kein Rest mehr besteht, speichere das Wort als Ergebnis am Knoten.
Man erkennt: Mit jedem Lauf durch die Methode wird das Suchwort kürzer, bis es komplett im Baum verteilt ist. Das ist es schon. Mehr braucht man nicht, um einen einfachen Präfixbaum aufzubauen. Die erste Etappe ist geschafft. Schaut man sich das Ergebnis im Debugger an (Breakpoint in der index_and_search-Methode auf die Zeile mit dem return-Statement setzen, kann man für das Feld root_node die Gesamtstruktur gut erkennen:
root_node = {TrieNode} <simple_trie.TrieNode object at 0x7fb69e0c1b70>
_TrieNode__children = {dict} {'W': <simple_trie.TrieNode object at 0x7fb69e0c1cf8>, 'H': <simple_trie.TrieNode object at 0x7fb69e0c1c18>}
__len__ = {int} 2
'H' (140422312369096) = {TrieNode} <simple_trie.TrieNode object at 0x7fb69e0c1c18>
_TrieNode__children = {dict} {'A': <simple_trie.TrieNode object at 0x7fb69e0c1cc0>}
__len__ = {int} 1
'A' (140422312369264) = {TrieNode} <simple_trie.TrieNode object at 0x7fb69e0c1cc0>
_TrieNode__children = {dict} {'U': <simple_trie.TrieNode object at 0x7fb69e0c1f60>, 'L': <simple_trie.TrieNode object at 0x7fb69e0c1d68>}
__len__ = {int} 2
'L' (140422312369432) = {TrieNode} <simple_trie.TrieNode object at 0x7fb69e0c1d68>
_TrieNode__children = {dict} {'L': <simple_trie.TrieNode object at 0x7fb69e0c1e10>}
__len__ = {int} 1
'L' (140422312369600) = {TrieNode} <simple_trie.TrieNode object at 0x7fb69e0c1e10>
_TrieNode__children = {dict} {'O': <simple_trie.TrieNode object at 0x7fb69e0c1e80>}
__len__ = {int} 1
'O' (140422312369712) = {TrieNode} <simple_trie.TrieNode object at 0x7fb69e0c1e80>
_TrieNode__children = {dict} {}
__len__ = {int} 0
_TrieNode__result = {str} 'HALLO'
_TrieNode__result = {NoneType} None
_TrieNode__result = {NoneType} None
'U' (140422312369936) = {TrieNode} <simple_trie.TrieNode object at 0x7fb69e0c1f60>
_TrieNode__children = {dict} {'S': <simple_trie.TrieNode object at 0x7fb69e0c1fd0>}
__len__ = {int} 1
'S' (140422312370048) = {TrieNode} <simple_trie.TrieNode object at 0x7fb69e0c1fd0>
_TrieNode__children = {dict} {}
__len__ = {int} 0
_TrieNode__result = {str} 'HAUS'
_TrieNode__result = {NoneType} None
_TrieNode__result = {NoneType} None
_TrieNode__result = {NoneType} None
'W' (140422312369208) = {TrieNode} <simple_trie.TrieNode object at 0x7fb69e0c1cf8>
_TrieNode__children = {dict} {'E': <simple_trie.TrieNode object at 0x7fb69e0d3080>, 'A': <simple_trie.TrieNode object at 0x7fb69e0d3240>}
__len__ = {int} 2
'A' (140422312440304) = {TrieNode} <simple_trie.TrieNode object at 0x7fb69e0d3240>
_TrieNode__children = {dict} {'S': <simple_trie.TrieNode object at 0x7fb69e0d32e8>}
__len__ = {int} 1
'S' (140422312440472) = {TrieNode} <simple_trie.TrieNode object at 0x7fb69e0d32e8>
_TrieNode__children = {dict} {'S': <simple_trie.TrieNode object at 0x7fb69e0d3390>}
__len__ = {int} 1
'S' (140422312440640) = {TrieNode} <simple_trie.TrieNode object at 0x7fb69e0d3390>
_TrieNode__children = {dict} {'E': <simple_trie.TrieNode object at 0x7fb69e0d3438>}
__len__ = {int} 1
'E' (140422312440808) = {TrieNode} <simple_trie.TrieNode object at 0x7fb69e0d3438>
_TrieNode__children = {dict} {'R': <simple_trie.TrieNode object at 0x7fb69e0d34a8>}
__len__ = {int} 1
'R' (140422312440920) = {TrieNode} <simple_trie.TrieNode object at 0x7fb69e0d34a8>
_TrieNode__children = {dict} {}
__len__ = {int} 0
_TrieNode__result = {str} 'WASSER'
_TrieNode__result = {NoneType} None
_TrieNode__result = {NoneType} None
_TrieNode__result = {NoneType} None
_TrieNode__result = {NoneType} None
'E' (140422312369880) = {TrieNode} <simple_trie.TrieNode object at 0x7fb69e0d3080>
_TrieNode__children = {dict} {'L': <simple_trie.TrieNode object at 0x7fb69e0d3128>}
__len__ = {int} 1
'L' (140422312440024) = {TrieNode} <simple_trie.TrieNode object at 0x7fb69e0d3128>
_TrieNode__children = {dict} {'T': <simple_trie.TrieNode object at 0x7fb69e0d3198>}
__len__ = {int} 1
'T' (140422312440136) = {TrieNode} <simple_trie.TrieNode object at 0x7fb69e0d3198>
_TrieNode__children = {dict} {}
__len__ = {int} 0
_TrieNode__result = {str} 'WELT'
_TrieNode__result = {NoneType} None
_TrieNode__result = {NoneType} None
_TrieNode__result = {NoneType} None
_TrieNode__result = {NoneType} None
Jetzt fehlt uns noch die Implementierung der Suche in der Methode search der TrieNode-Klasse. Auch hier konnte man den grundsätzlichen Ablauf schon in der weiter oben dargestellten Animation sehen.
Auf der Code-Seite sieht das dann so aus:
def search(self, word: str) -> list:
results = [] # 1.
if len(word) > 0: # 2.
letter = word[0].upper() # 3.
if letter in self.__children.keys(): # 4.
results.extend(self.__children[letter].search(word[1:])) # 5.
else: # 6.
if self.__result is not None: # 7.
results.append(self.__result) # 8.
[results.extend(self.__children[key].search('')) for key in self.__children.keys()] # 9.
return results # 10.
In Worten:
- Lege eine neue leere Ergebnisliste an.
- Ist vom Suchwort noch etwas übrig?
- Wenn ja, nehme den ersten Buchstaben als Großbuchstaben,
- und wenn dazu ein Kindknoten existiert,
- erweitere die Ergebnisliste mit den Ergebnissen der Suchfunktion des Kindknotens, aufgerufen mit dem Wort ohne dem ersten Buchstaben.
- Falls vom Wort nichts mehr übrig ist,
- prüfe, ob der Knoten ein Ergebnis hat,
- und füge es, falls vorhanden, der Ergebnisliste hinzu.
- Außerdem durchlaufe alle weiteren Kinder und erweitere die Ergebnisliste um die Ergebnisse, die von der Suchmethode der Kinder bei einem leeren Restwort geliefert werden. So werden rekursiv alle Ergebnisse erfasst, die an allen weiteren Kindknoten hängen.
- Liefere die Ergebnisliste zurück.
Für die ganz Schreibfaulen liegt der komplette Source Code von simple_trie.py in einem GitHub-Gist.
Test it!
Ruft man nun wieder die Doctest-Tests auf (python3.5 -m doctest -v simple_trie.py, -v hier für mehr Ausgabe), so erhält man diese erfreuliche Nachricht:
Trying:
set(index_and_search(['Hallo', 'Haus', 'Welt', 'Wasser'], 'hau')) == {'HAUS'}
Expecting:
True
ok
Trying:
set(index_and_search(['Hallo', 'Haus', 'Welt', 'Wasser', 'HAL 8999'], 'hal')) == {'HALLO', 'HAL 8999'}
Expecting:
True
ok
Trying:
index_and_search(['Hallo', 'Haus', 'Welt', 'Wasser', 'HAL 8999'], 'sonne')
Expecting:
[]
ok
6 items had no tests:
simple_trie
simple_trie.TrieNode
simple_trie.TrieNode._TrieNode__add
simple_trie.TrieNode.__init__
simple_trie.TrieNode.add
simple_trie.TrieNode.search
1 items passed all tests:
3 tests in simple_trie.index_and_search
3 tests in 7 items.
3 passed and 0 failed.
Test passed.
Jetzt kennen wir die Grunddatenstruktur. Damit geht natürlich noch mehr – das kommt aber dann in späteren Beiträgen dran.
Autor:
Jürgen Edelbluth
Themen:
Software-Entwicklung Python
Veröffentlicht:
23.10.2016 14:12
Zuletzt aktualisiert:
13.03.2020 16:57